小学2年生の算数のプリントがスゴイ…“九九を図にした法則”が美しすぎると話題に!
今、Twitterで話題になっている“九九を図にした法則”。知らずにただ暗記していたけれど、こんなに美しいものだったなんて…(記事提供 FUNDO)
Twitterユーザーであり、毎日新聞 統合デジタル取材センターの大村健一さんがツイートした、小学2年生の算数のプリントが話題です!
筆者はこんな問題がとけたら、もう少し算数が好きになっていたかも!などと根拠のない言い訳をしつつ久々にじっくり考えてしまいました。
知り合いの母親から見せてもらった小学2年生の算数のプリント。「九九って36種類しか数がないの不思議だよな」というツイートがここ最近は話題で、それを見たときも驚きでしたが、こうして図にしてみるとすごく美しい。教材を考えた人、すごいわ。とにかく感動してしまったので、許可を得てアップ。
出典:twitter.com

綺麗な図が出来ていることから、規則性がありそうですね。
問題をよんでみると…
2の段を例にあげると、2×1=2、2×2=4、「2」→「4」など、答えの順番に線を繋いでいくということですね。

どうやら、規則性があるらしい
こんにちは(⌒ω⌒ )
出典:twitter.com
1と9、2と8、3と7、4と6が同じ形になるの面白いですね。
しかも、お互い逆回転ですよね!
10進数ならではということか。
上のツイートが面白そうでしたので、分かりやすく図を並べてみました。
【1の段と9の段が同じ形】
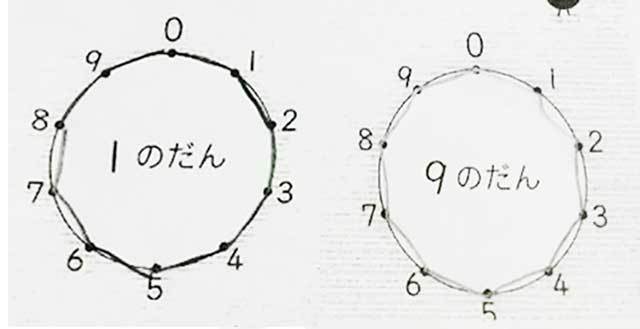
【2の段と8の段が同じ形】
2の段→2×1=1、2×2=4、順に点を繋ぐと、右回り。
9の段→8×1=8、8×2=16、8×3=24、下一桁「8」→「6」→「4」と順に点を繋ぐと、左周り。
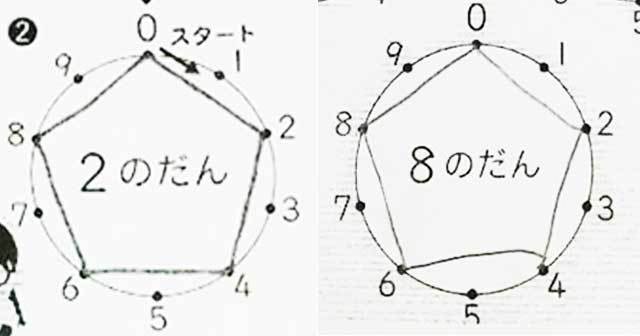
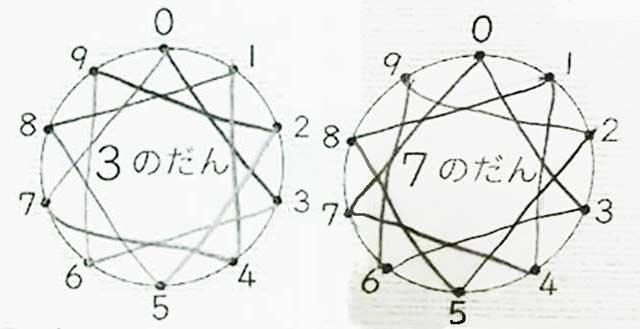
【3の段と7の段が同じ形】
3の段→3×1=3、3×2=6、順に点を繋ぐと、右回り。
7の段→7×1=7、7×2=14、7×3=21、下一桁「7」→「4」→「1」と順に点を繋ぐと、左周り。
【4の段と6の段が同じ形】
4の段→4×1=4、4×2=8、順に点を繋ぐと、右回り。
7の段→6×1=6、6×2=12、6×3=18、下一桁「6」→「2」→「8」と順に点を繋ぐと、左周り。

なるほど!これでスッキリ解りました!!こんな法則性があったとは驚きですね。しかも共通の図形が出来ている所が神秘的…。
さらに、こんなツイートも!
九九はひたすら暗記で覚えた記憶しかないので、図形にするという発想がすごい!と、衝撃でした。
出典:twitter.com
そして、これ、面白い!!
九九はただ暗記する少しつらいものでした。
出典:twitter.com
楽しみながら興味を持って勉強できること素晴らしいですね。
そして、すでにこの図を見たことがある方からのツイート
さっき帰って来たうちの子にこの図をみせたら、
出典:twitter.com
「これ今日習ってきた!」
見ると、全く同じものが東京書籍の「新しい算数 3上」に、二年生の復習としてカラーで載っています。
こんな風に教えてほしいなあ…と思っていたら、もうちゃんと教科書に載ってるんですね。よかったです♪
ルドルフ・シュタイナーが提唱したシュタイナー教育ですねぇ(かけ算の糸かけ)
出典:twitter.com
いかがでしたか?ツイートされた大村さんも「自分の未知の数学の領域まで行ってしまった」とおっしゃるほど、九九の図形のツイートが盛り上がっていました。中には、立体3Dにしたり、ピラミット型にしたりして、さらなる発展が…。ご興味のある方は、大村さんのツイートをぜひご覧ください!
関連記事はこちらから
みなさんは九九ってどうやって覚えました?我が家は歌を歌いながら覚えましたが、こちらのお家の娘さんはユニークな覚え方をしているようですよ!!
九九を知らないからこそ、方程式を知らないからこそ…自分の知っていることで問題を解こうとする子供の柔軟な発想に、脱帽です(記事提供 FUNDO)


























